In the article on Tensile Testing there is brief description of Young’s Modulus (also called the Elastic Modulus or Modulus of Elasticity).  Every now and again a question is raised as to whether it is possible to change this material characteristic, usually because designers are looking for more stiffness in a particular structure.  Hence, a discussion on Young’s Modulus is provided.

When a metal is subjected to load in a tension test, there is an initial range of loading in which no permanent deformation of the specimen occurs, i.e. if the load is removed at any value within this range, the specimen will return completely to its original dimensions.  This is known as the elastic range.  The data obtained from the tension test is generally plotted as a stress-strain curve.  Within the elastic range of loading the strain produced is directly proportional to the applied stress.  The law of proportionality between stress and strain in the elastic range is known as Hooke’s Law.  The Young’s Modulus is the ratio between the stress that is applied (tensile or compressive) and the elastic strain that results, i.e. it is the slope of the elastic portion of the stress-strain curve and is expressed in units of stress (psi).  The higher the modulus, the more stress is needed to create the same amount of strain, i.e. the higher the modulus the higher the stiffness or rigidity of the material.  Since Young’s Modulus is needed, in conjunction with thickness, for calculating deflection of beams and other members, it is an important design value. 

Young’s Modulus is determined by the binding forces between atoms.  Since these forces cannot be changed without changing the basic nature of the material, it follows that the Young’s Modulus is one of the most structure-insensitive of the mechanical properties.  It is only slightly affected by alloying additions, heat treatment, cold work, or, in the case of steel, by relatively exotic microstructures such as dual phase.  The tensile Young’s Modulus of ferritic steels is close to 30,000,000 psi at room temperature.  The tensile Young’s Modulus of austenitic stainless steels is about 28,000,000 psi at room temperature. Within each material class there are very small differences. Increasing the temperature decreases the Young’s Modulus.  It decreases linearly to somewhere in the order of 1000^oF, depending on material class, and then begins to drop rapidly.

Because the stress-strain relationship of many materials does not conform to Hooke’s Law throughout the elastic range, there are several methods of defining the Young’s Modulus as a straight line relationship using an approximation such as an initial tangent modulus, a tangent modulus at any stress, a secant modulus between the origin and any stress, and a chord modulus between any two stresses.  An ASTM standard exists for test methods.

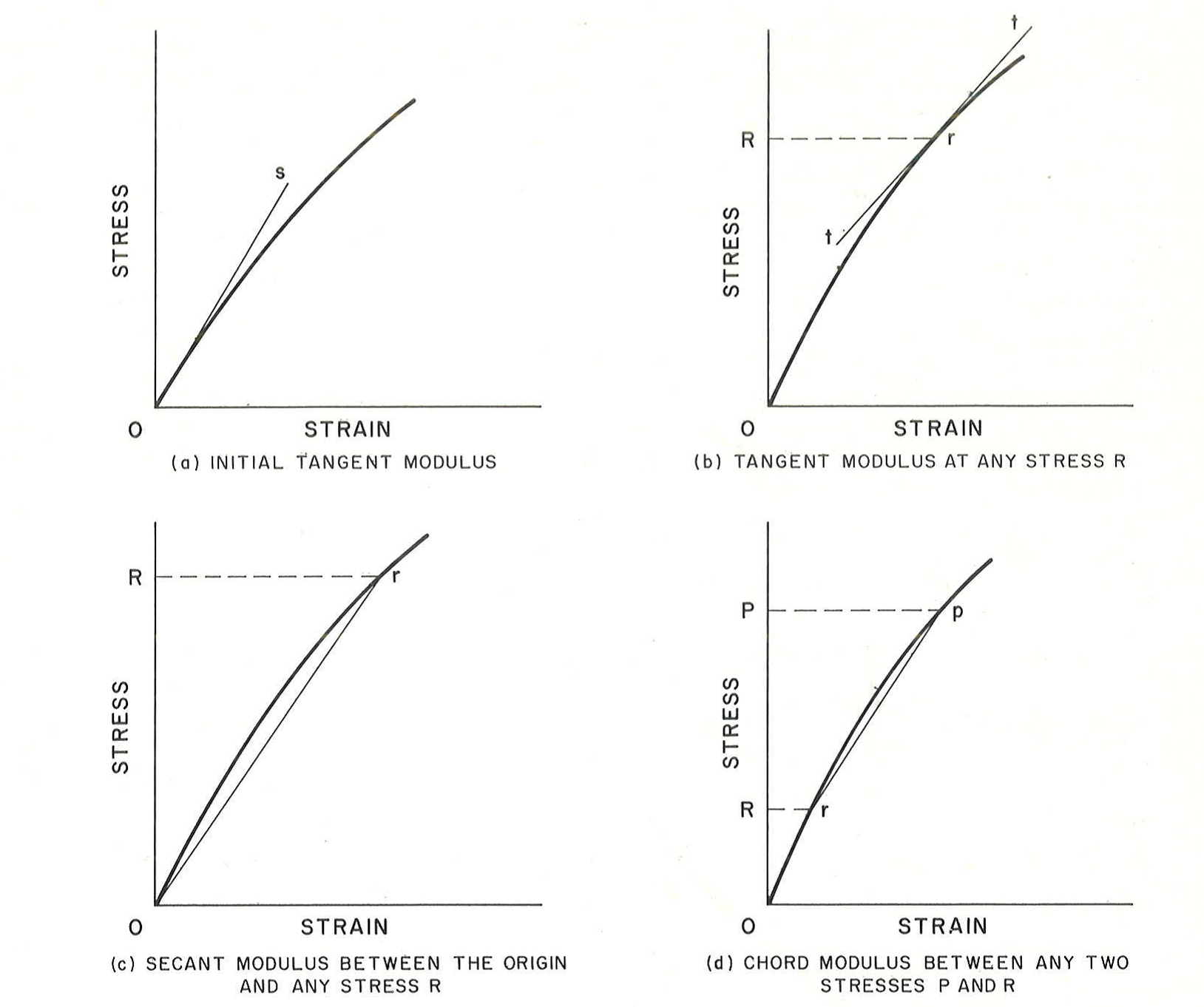
Although Young’s Modulus is a characteristic of the stress-strain curve, its precise determination using static methods (deflection under load increments in a tension test) requires regard for numerous variables, including the accuracy and the precision of the apparatus used to measure stress and strain, characteristics of the test specimen (such as grain orientation relative to the direction of stress, grain size, residual stress, previous strain history, dimensions and eccentricity), testing conditions (such as alignment of the specimen, speed of testing, temperature, and temperature variations) and interpretation of the test data. Following the ASTM standard ensures far more accurate results than taking the number off a routine stress-strain curve.  However, the more accurate methods are dynamic in nature and are based in induced mechanical vibration or ultrasonic pulses where the mode and period of vibration of a metal specimen are obtained and analyzed.